Basic Phiscally Rules on Quadcopters
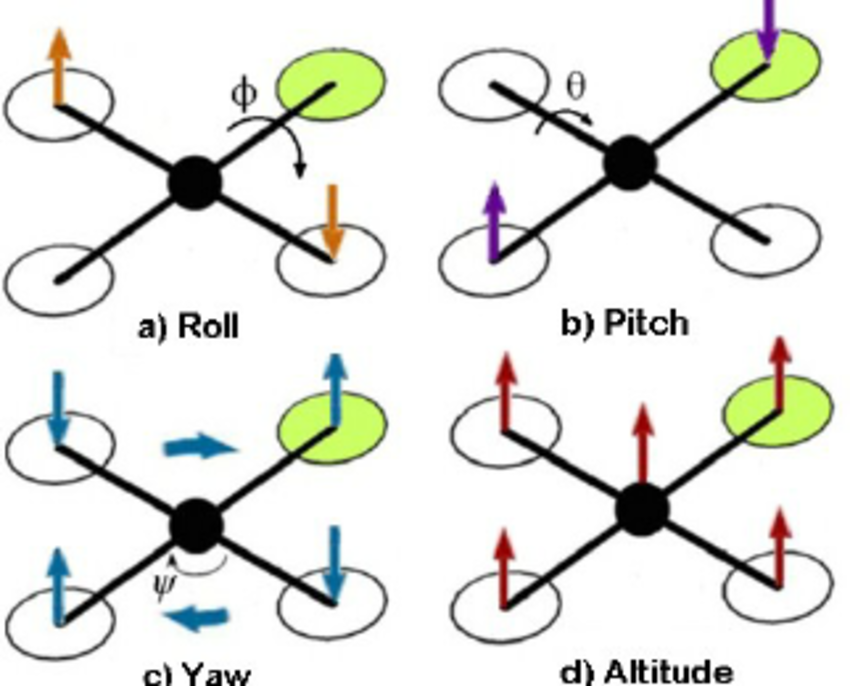
To ensure that the Quadrotor system remains stable, most importantly, it must lie flat on the ground. This requires some knowledge of the physics of the system, as well as some controller designs. <div><p>To start, we need to define some variables to be controlled. Below is a diagram of the quad-copter with some definitions.</p> </div> <div><p>Before we starting, we need to define some variables to check. Below is a quadcopter figure with some of definitions.</p></div> <div><a class="img-thumbnail img-thumbnail-no-borders d-block lightbox" href="https://thecodeprogram.com/img/contents/2019/11/quadrotor-axis.jpg" data-plugin-options="{'type':'image'}"><img class="img-fluid" src="https://thecodeprogram.com/img/contents/2019/11/quadrotor-axis.jpg" alt="Quadrotor Axis"><span class="zoom"><i class="fas fa-search"></i></span></a></div> <div><p>As you can see, the Euler Pitch and Roll angles are used to explain how the system is oriented laterally and how the Yaw angle rotates. For a stable flight, all of this angles must be in stable position.</p></div> <div><p>The controller of drone will decide RPM values of engines. For changing roll angle number 1 and number 3 engines together, number 2 and number 4 engines RPM values must be changed. Th change pitch value all engines RPM values must be changed.</p></div> <div><p>The yaw rotation is uses engines centrifugal forces. As we can see below pictures mutul both engines have same rotation direction. One pair of motor will rotate Clock Wise, other pair will rotate Counter Clock Wise. </p></div> <div><br /><a class="img-thumbnail img-thumbnail-no-borders d-block lightbox" href="https://thecodeprogram.com/img/contents/2019/11/quadrotor-motor-rotations.jpg" data-plugin-options="{'type':'image'}"><img class="img-fluid" src="https://thecodeprogram.com/img/contents/2019/11/quadrotor-motor-rotations.jpg" alt="Quadrotor Motor Rotations"><span class="zoom"><i class="fas fa-search"></i></span></a></div> <div><p>Newton's third law says : every force have an equal and opposite force. Applying a torque to the parts applies a torque along the drone. It also gives the controller the ability to influence the stretching position. Qualitatively, this seems good; But, these principles must be measured to design a flight controller.</p></div> <div><p>Using a free body diagram to obtain some dynamic equations will always help. The following example shows the forces that influence rotation from the rear viewpoint in rolling.</p></div> <div><br /><a class="img-thumbnail img-thumbnail-no-borders d-block lightbox" href="https://thecodeprogram.com/img/contents/2019/11/quadrotor-roll-and-pitch-perspective.png" data-plugin-options="{'type':'image'}"><img class="img-fluid" src="https://thecodeprogram.com/img/contents/2019/11/quadrotor-roll-and-pitch-perspective.png" alt="Quadrotor Roll and Pitch Perspective"><span class="zoom"><i class="fas fa-search"></i></span></a></div> <div><p>At each end of the plane there is gravity that pulls the center of mass and two thrust forces down. The thrust forces are divided into two parts: duty cycle and proportion constant kf. The duty cycle is the value 0-1, which is calculated by the controller and represents the minimum and maximum pressure. The proportionality constant represents the transformation of power between the duty cycle (circuit and air dynamics are not considered).</p></div> <div><p>Equasition of sum of moments is below : </p></div> <div><p class="has-medium-font-size">L * k(i<span style="font-size:8px">2</span > + i<span style="font-size:8px">4</span >) - L * k(i<span style="font-size:8px">1</span > + i<span style="font-size:8px">3</span >) = I<span style="font-size:8px">roll</span > * (angle value)</p></div> <div><p>The same equations can be applied to the pitch variable because the drone is symmetrical on both sides. For the wobble movement, it is only slightly different. Below is a diagram showing the torques generated by each engine. It means that the motor rotates clockwise, that is, the counter-torque felt by the drone is counter-clockwise.</p></div> <div><br /><a class="img-thumbnail img-thumbnail-no-borders d-block lightbox" href="https://thecodeprogram.com/img/contents/2019/11/quadrotor-yaw-perspective.png" data-plugin-options="{'type':'image'}"><img class="img-fluid" src="https://thecodeprogram.com/img/contents/2019/11/quadrotor-yaw-perspective.png" alt="Quadrotor Yaw Perspective"><span class="zoom"><i class="fas fa-search"></i></span></a></div> <div><p>Equasition of sum of torques is below : </p></div> <div><p class="has-medium-font-size">L * k(i<span style="font-size:8px">1</span > + i<span style="font-size:8px">4</span >) - L * k(i<span style="font-size:8px">2</span > + i<span style="font-size:8px">3</span >) = I<span style="font-size:8px">yaw</span > * (angle value)</p></div> <div><p>Because the drone is simple and linear, it is quite simple to obtain these equations. But, it is important to understand them, especially when it comes to designing the controller. Current sensory feedback of controller design, noise, digitization constraints and consider the structure and physical dynamics of the embedded system.</p></div> <div><p>Burak Hamdi TUFAN</p></div>Tags
Share this Post
Author
I am a software developer experienced 15 years and here to share all my programming experiences. I have worked on so many platforms and programming languages especially C, C#, C++ and Java. I am studing PhD at Kocaeli University on Aviation Technologies. I am building softwares and technologies on aviation.
09/03/2020
Explanation of Creational Design Patterns
05/04/2020
Explanation of Facade Design Pattern
11/06/2020
Comments