Explanation of Visitor Design Pattern

Hello everyone, in this article we are going to talk about Visitor Design Pattern within Behavioral Design Patterns. We will talk first on its description then make an example in C# and Visual Studio.

Let's get started.

Visitor Design Pattern allows the developer to add new features to the class without any changing on hierachy and the structure in the existing class. We build a loosen link between features and classes with Visiyor Design Pattern.

For example we may sometimes have an abstract class or an interface to derive classes which accomodate some requirements. Also we may want to add some new features to our class or classes. This will lead us to change the entire class structure or the interface through adding the behaviours which equired by these new features but not required for the entire class. We do not want to see these not required behaviours in other classes. To prevent this we create a Visitor interface or abstract class and we add these behaviours into it. Then we derive new features from this class.

This design patern is complex a little bit. So let's start to talk on an example directly.

Below image you can see the schematic of my example

In here first I will create my Feature interface and then derive the features from this interface. Below code blocks you will see the feature interface and feature classes.

IFeature.cs


namespace VisitorPattern_Example
{
    public interface IFeature
    {
        void EnableFeature(IAircraft aircraft);
    }
}

IFE.cs


using System;

namespace VisitorPattern_Example
{
    class IFE : IFeature
    {
        public void EnableFeature(IAircraft aircraft)
        {
            if (aircraft is B777)
            {
                Console.WriteLine("IFE is enabled");
            }
            else if (aircraft is B777F)
            {
                Console.WriteLine("IFE is not required for Cargo Aircrafts...");
            }
        }
    }
}

CargoCooling.cs


using System;

namespace VisitorPattern_Example
{
    class CargoCooling : IFeature
    {
        public void EnableFeature(IAircraft aircraft)
        {
            if (aircraft is B777)
            {
                Console.WriteLine("Cargo Cooling is enabled");
            }
            else if (aircraft is B777F)
            {
                Console.WriteLine("Corgo Cooling is not required for Cargo Aircrafts...");
            }
        }
    }
}

Now I will create an interface for concrete classes and then I will derive the concrete classes from this interface. Below you will see the interface and the other concrete classes which derived from this interface.

IAircraft.cs


namespace VisitorPattern_Example
{
    public interface IAircraft
    {
        void ActivateFeature(IFeature features);
    }
}

B777.cs


using System;

namespace VisitorPattern_Example
{
    class B777 : IAircraft
    {
        public B777()
        {
            Console.WriteLine("B777 is initializing...");
        }

        public void ActivateFeature(IFeature features)
        {
            features.EnableFeature(this);
        }
    }
}

B777F.cs


using System;

namespace VisitorPattern_Example
{
    class B777F : IAircraft
    {
        public B777F()
        {
            Console.WriteLine("B777F is initializing...");
        }

        public void ActivateFeature(IFeature features)
        {
            features.EnableFeature(this);
        }
    }
}

All of configurations are ready. Now I will initialize the concrete classes and belonged features from our program main function.

Program.cs


using System;

namespace VisitorPattern_Example
{
    class Program
    {
        static void Main(string[] args)
        {
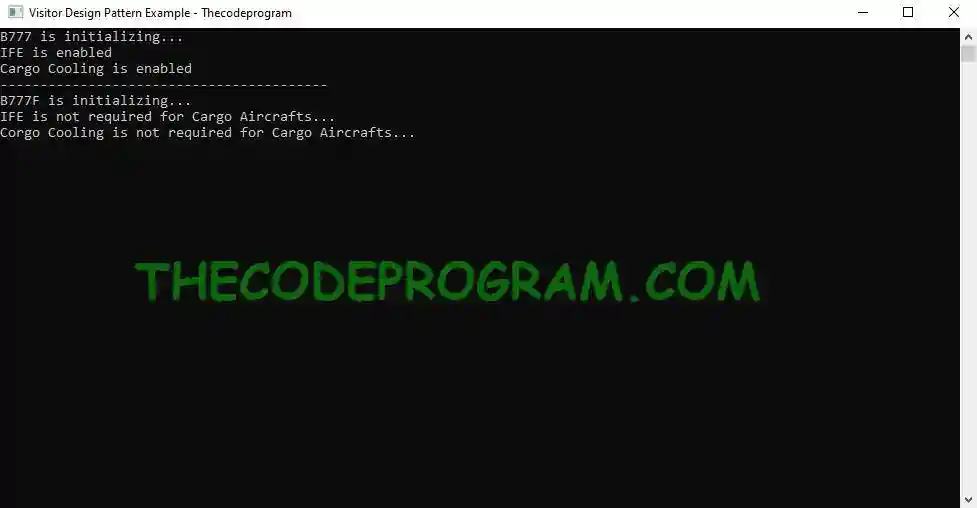
            Console.Title = "Visitor Design Pattern Example - Thecodeprogram";
            //Features Arrasy
            IFeature[] listFeatures = { new IFE(), new CargoCooling() };

            //Concrete classes to initialize class and features
            B777 _b777 = new B777();
            for (int i = 0; i < listFeatures.Length; i++)
            {
                _b777.ActivateFeature(listFeatures[i]);
            }
            
            Console.WriteLine("-----------------------------------------");

            B777F _b777f = new B777F();
            for (int i = 0; i < listFeatures.Length; i++)
            {
                _b777f.ActivateFeature(listFeatures[i]);
            }

            Console.ReadLine();
        }
    }
}

Below image you can see the output of the program.

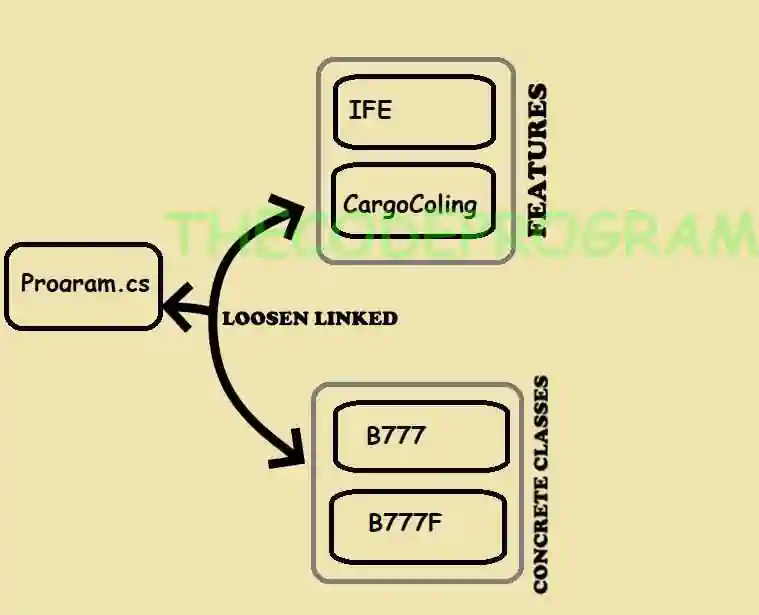
In this way the all concrete classes and the features classes have been loosen linked and we can add new features without any changing in any other classes.

That is all in this article.

You can reach the example application on Github via : https://github.com/thecodeprogram/VisitorPattern_Example

Have good visiting the classes

Burak Hamdi TUFAN

Share this Post

Send with Whatsapp

Author

Burak Hamdi TUFAN

I am a software developer experienced 15 years and here to share all my programming experiences. I have worked on so many platforms and programming languages especially C, C#, C++ and Java. I am studing PhD at Kocaeli University on Aviation Technologies. I am building softwares and technologies on aviation.

Facebook Twitter Instagram LinkedIn Youtube